Asymptotic Notation

• The mathematical language on resource analysis and worst case analysis.

Visual Definition of Big O notation

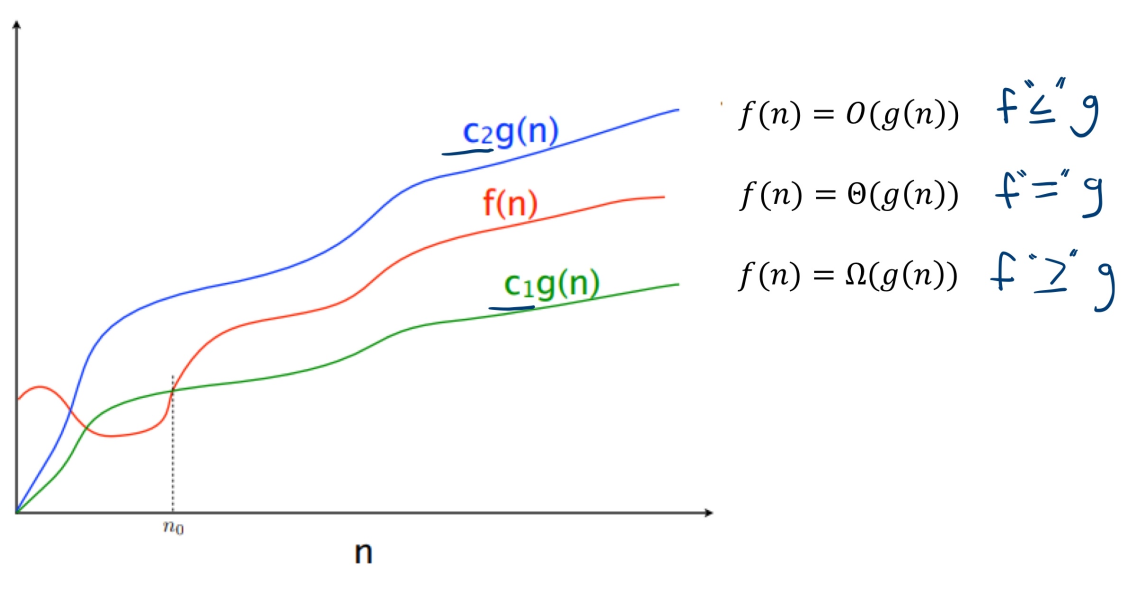
• Explanation
  • $f(n)=O(g(n))$ → $f\le g$ ($f$ is upper bounded by $g$)
    • $f(n)\in O(g(n))$
  • $f(n)=\Theta (g(n))$ → $f=g$ ($f$ is tight bounded by $g$)
  • $f(n)=\Omega (g(n))$ → $f\ge g$ ($f$ is lower bounded by $g$)
• Terminology
  • $n_0$
    • (1st input) we only care about what happens after this
  • $f(n)$ - some function we’re analyzing
  • $g(n)$ - the “benchmark” function you’re comparing to
    • $c_{1}g(n)$ & $c_{2}g(n)$ - the same function $g(n)$ but scaled up/down by constants
    • Multiplying by $c$ tilts the $g(n)$ up/down, but it doesn’t change the fundamental structure or shape of $g(n)$
• Explaining the graph
  • Tight bounded relationship
    • If you can find constants $c_1$ and $c_2$ such that $c_{1}g(n)\le f(n)\le c_{2}g(n)$ for large $n$, then $f(n)$ “grows like” $g(n)$ and we say $f(n)=\Theta (g(n))$.
    • When graphs are tightly bounded, they share same growth rate
    • So if we can prove if 2 graphs are tightly bounded, we know they share the same growth rate, hence we can say $f(n)=\Theta (g(n))$
  • This is why we ignore constants in asymptotic notation because they just stretch or shrink the graph vertically, but don’t change the fundamental growth rate
    • We’re interested in the dominant term, not the coefficients.

Small Example

f(n) = 3n + 50
g(n) = n

• Question: “Does $f(n)$ grow similarly to $g(n)$?”
• If $f(n)$ always stays between $c_1\cdot g(n)$ and $c_2\cdot g(n)$ after some $n_0$, then it’s Θ(g(n)).
  • Constants like 3 and 50 in f(n) don’t affect asymptotic growth — they just shift or scale the curve.
  • This is why in Big-O/Theta/Ω we drop constants and lower-order terms.
    • (Example: f(n) = 3n + 50 becomes Θ(n))

Asymptotic Notation

These functions are all different ways of doing an asymptotic comparison ⇒ An asymptotic comparison of functions

• $O(g(n))$
  • $f\in O(g(n))\equiv \exists c>0,\exists n_0>0,\forall n\ge n_0,f(n)\le c\ast g(n)$
  • The set of functions with asymptotic behavior less than or equal to $g(n)$
    • $f(n)\in O(g(n))$
  • Upper-bounded by $c\ast g(n)$ for large enough values $n$
    • Eventually, $c\ast g(n)$ will become and stay bigger after $n_0$ ⇒ An algorithm whose running time is $f(n)$ will eventually do fewer operations than an algorithm whose running time is $g(n)$.
    • An algorithm whose running time is $f(n)$ is faster than an algorithm whose running time is $g(n)$
• $\Theta (g(n))$
  • $\Omega (g(n))\cap O(g(n))$
  • “Tightly” within constant of $g$ for large $n$
  • You satisfy the upper/lower bound
• $\Omega (g(n))$
  • $f\in \Omega (g(n))\equiv \exists c>0,\exists n_0>0,\forall n\ge n_0,f(n)\ge c\ast g(n)$
  • The set of functions that has this asymptotic behavior greater than or equal to $g(n)$
  • Lower-bounded by a constant times $g$ for large enough values $n$

Examples

Example 1

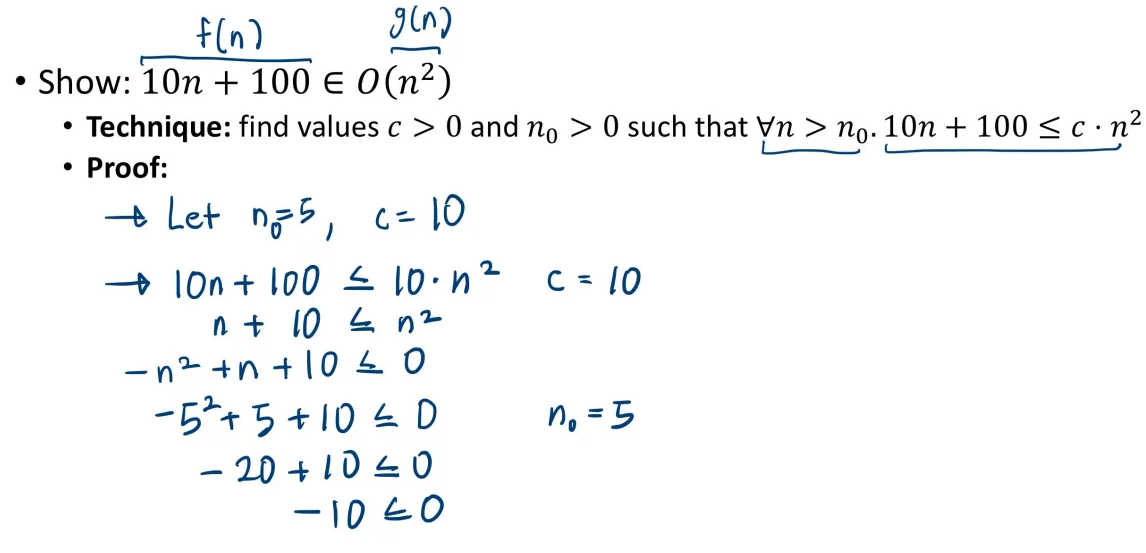
• We’re proving if $10n+100$ is smaller than $n^2$ (if it belongs to the set $O(n^2)$)
• Since we have $\exists c>0$ and $\exists n_0>0$ for $O(g(n))$, we can pick arbitrary values greater than 0 for $c$ and $n_0$
• what this means
  • Eventually, $10n+1$ will grow slower than some constant multiple of $n^2$ starting from $n_0$.
  • The relationship doesn’t flip after that $n_0$ — $10n+100$ never overtakes $c\cdot n^2=10n^2$ again.
    • We have $\forall n>n_0$ , so once we find $n_0$ it will work for all $n$

Example 2

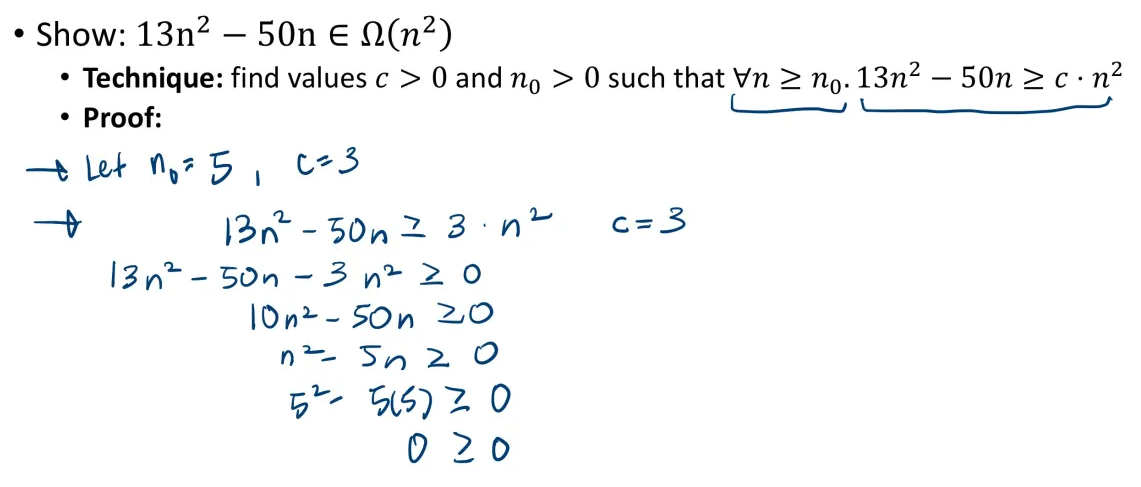
Example 3

• It’s a contradiction because $c\ge n$ must hold when $n\to \infty$ and $c$ is a constant

Gaining intuition

• When doing asymptotic analysis of functions
  • If multiple expressions are added together, ignore all but the biggest
  • Ignore all multiplicative constants
  • Ignore bases of logs
  • Do NOT ignore
    • non multiplicative and non-additive constants (ex. in exponents, bases of exponents)
    • logarithms themselves
• Examples
  • $4n+5$ → O(n)
  • $0.5n\log n+2n+7$ → O(n log n)
  • $n^3+2^n+3n$ → O(2^3)
  • $n\log (10n^2)$ → O(n log n)