leejunkim

Worst Case Analysis

3 min read

Definition

What is the worst case use of the resources compared to the input size?

  • resource analysis, on the other hand, is just some way of associating the amount of resources you need compared to the size of input
  • By focusing on the worst-case, we get a performance guarantee. We can say that for any input of size n, the algorithm will never use more resources than what our function f(n) predicts.
  • one of the ways we could define f(n) (when we’re trying to define how the input size relates to the amount of time spent)
    • worst case analysis is the most common
  • If an algorithm has a worst case running time of f(n)
    • Among all possible size-𝑛 inputs, the “worst” one will do f(n) “operations” • I.e. f(n) gives the maximum operation count from among all inputs of size
    • We say of all of the input of size n, which one takes the most time?
  • Questions to ask
    • What are the units of the input size?
      • # items in the list
      • length of variable n
    • What are the operations we’re counting?
      • Think what will be most important for actually doing the work of the algorithm
      • What operation is the most expensive?
      • ex) arithmetic
    • For each line
      • How many times will it run?
      • How long does it take to run?
      • Does this change with the input size?
  • Rule of thumb
    • ignore constants (non-dominant terms)
    • ignore small behaviors for small inputs (use long-term input behavior)
    • When counting the # of operations, we count the operation that happens the most often

Example 1 (simple)

def linear_search(arr, x):
    for item in arr:
        if item == x:
            return True
    return False

Worst Case Running Time Analysis

Worst-case time is the maximum amount of time (steps/operations) the algorithm could take for any input of size n.

  • worst case
    • x is not in the list, we much check every element
  • how many operations
    • n comparisons
  • worst-case time complexity = O(n)

Worst Case Space Analysis

Worst-case space is the maximum additional memory (not counting input) used by the algorithm.

  • what extra space do we use
    • We just use one variable (item) and maybe a few booleans internally.
  • Worst-case space complexity = O(1)
    • (Constant space, no matter how big the input list is.)

Example 2

Example a

  • in if-else cases
    • pick the worse branch (don’t forget to also count the if case haha)
  • But in all honesty, counting EVERYTHING is tedious, so the rule of thumb is that we ignore the non-deterministic terms

Example b

  • i++, .add, j++ all happens as much or less than the print statements
    • Anything that happens as much as another operation, the count will only increase by a constant
    • So just “group” them as one

Example c

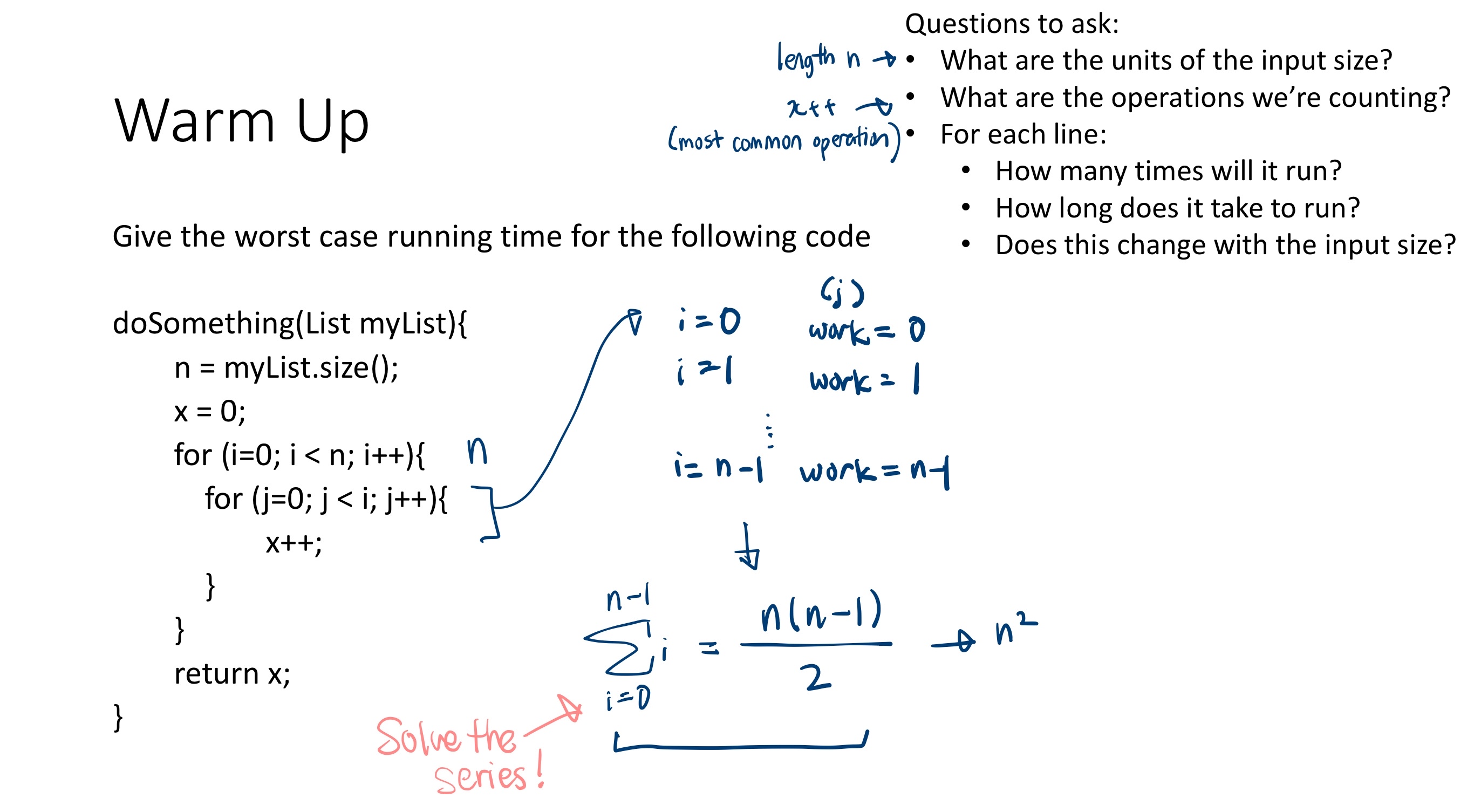
  • For this, we solved the series
  • We didn’t multiply one more n (outermost loop)
    • the inner loop already depends on the outer

Graph View

Backlinks