Overview
A way of comparing 2 sets of code.
- Let’s say code 1 and code 2 does exactly the same thing
- Compare them mathematically about how efficient they run
- In a coding interview, you will ABSOLUTELY BE ASKED QUESTIONS ABOUT THIS!!
- Time complexity
- theoretical, mathematical way to describe how the number of operations an algorithm performs grows as the input size (n) grows
- specifically designed to be independent of the machine
- Space complexity
- Code 1 is fast but takes a lot of space
- Code 2 is slower but it takes less memory
Big O Notations
- Chart
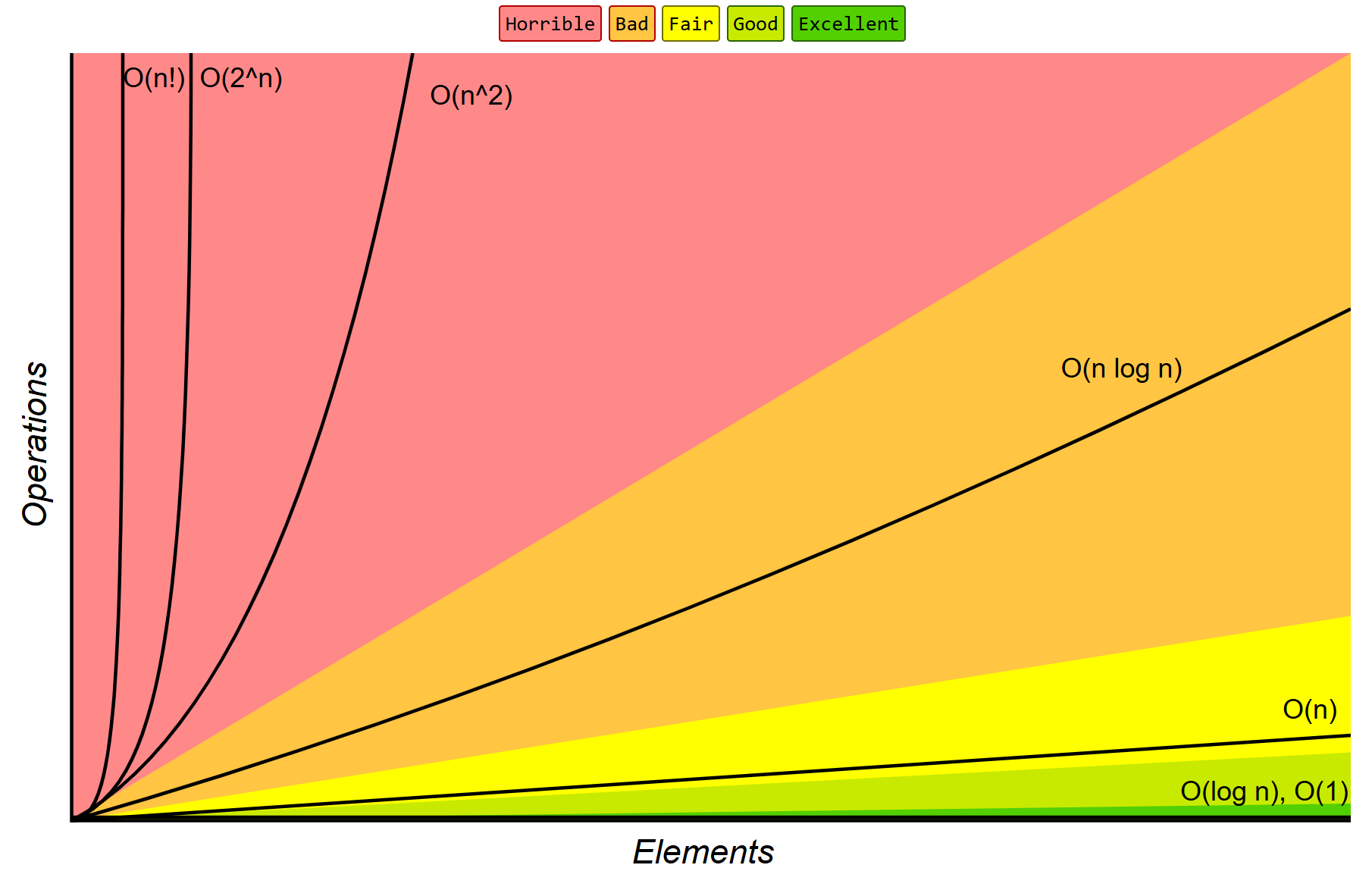
- We don’t cover the left 2
- We want to say in
O(n), O(log n), O(1)
- useful
O(1) - Constant time
- most efficient complexity
public static void addItems(int n) {
return n + 1;
}- it doesn’t matter how big the input
nis, there is always going to be one addition - as
ngrows, the number of operations stay the same
O(logn) - Logarithmic time
- As the input
ngrows exponentially (e.g., doubles), the number of operations only increases by one - This happens when an algorithm repeatedly divides the data in half with each step.
- Example: binary search, or finding an item in a Balanced Binary Search Tree
- Divide and Conquer
// A loop that demonstrates O(log n) behavior
// If n is 16, the loop runs 4 times (16 -> 8 -> 4 -> 2 -> 1)
// log₂(16) = 4
for (int i = 1; i < n; i = i * 2) {
System.out.println("Hello");
}O(n) - Linear time
- technically will always mean the worst case
public static void printItems(int n) {
for (int i = 0; i < n; i++) {
System.out.println(i);
}
for (int j = 0; j < n; j++) {
System.out.println(j);
}
}- The input is
n - Even though we have 2 for loops (2n), we drop the constant, so it becomes n
O(n logn) - Log-Linear Time
- This is a very common and efficient complexity for sorting algorithms. It’s often the result of performing an
O(log n)operationntimes.- quick sort
- merge sort
- Heap Sort
O(n^2) - Quadratic time
- The number of operations grows proportionally to the square of the input size
n.
public static void printItems(int n) {
// 1st for loop -> O(n^2)
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.println(i + " " + j);
}
}
// 2nd for loop -> O(n)
for (int k = 0; k < n; k++) {
System.out.println(k);
}
}- 1st for loop → a total of
n * n = n^2lines that were output - 2nd for loop →
O(n) - Total is
O(n^2 + n), but we drop the non dominants, so it becomesO(n^2)n^2grows much faster thann
Different terms for inputs
public static void printItems(int a, int b) {
for (int i = 0; i < a; i++) {
System.out.println(k);
}
for (int j = 0; j < b; j++) {
System.out.println(k);
}
}- You might mistake this for a total of
O(n) + O(n) = O(2n) -> O(n) - But this is actually
O(a + b)because it has different inputs! (you can’t just say they’re bothn)
With array lists
[11,3,23,7]
O(1)myList.add(17)→ add to backmyList.remove(4)(index) → remove back- have no re-indexing
- just have 1 operation
- Finding item by index
O(n)→nis number of itemsmyList.remove(0)→ remove the 1st element- Need to shift all elements forward
myList.add(0,11)→ add to front (0th index)- Need to shift all elements backward
- Finding item by value