Binary Heap

Binary

A complete binary tree that fulfills the heap properties (either a max-heap or min-heap)

• A specific type of heap
• A Priority queue data structure

• a complete binary tree:
  • binary → It’s called a binary heap because it is a Binary tree. You can have heaps that are not binary trees.
  • complete → All layers are full
• When people say “heap” in a data structures class, they almost always mean a binary heap, unless they explicitly say otherwise.

Height and nodes

• Maximum number of total nodes in a binary tree of height $h$
  • $2^{h+1}-1\approx \Theta (2^h)$ nodes
• Minimum height of a binary tree of $n$ number of nodes
  • $O(\log n)$
    • derived from $n=2^{h+1}-1$
• Heap Idea:
  • If $n$ values are inserted in a complete tree, the height will be roughly $\text{log }n$
  • Ensure each insert and deleteMin requires just one “trip” from root to leaf
• We will do one operation per level of our tree → this makes the amount of time we spend equal to the height of the tree

Binary Min Heap

• We maintain the “Min Heap Property” of the tree
  • Every node’s priority is $\le$ its children’s property
• Parents are more important than children

Represented as an array

Where is the min?

• Root is guaranteed to be the minimum value, so know the minimum value right away

Insert

insert(item) {
	put item in the "next open spot"
	// keep tree complete
	// perlocate up
	while (item.priority < parent(item).priority) {
		swap item with parent
	}
}

• Because we’re only comparing with the parent, at most we’re doing 1 operation per level of the tree, so the running time of this is the height of the tree ($\text{log }n$)​
• Illustration

deleteMin

deleteMin(){
	min = root
	br = bottom - right item
	move br to the root
	while(br > either of its children){
		swap br with its smallest child
		}
	return min
}

• Illustration
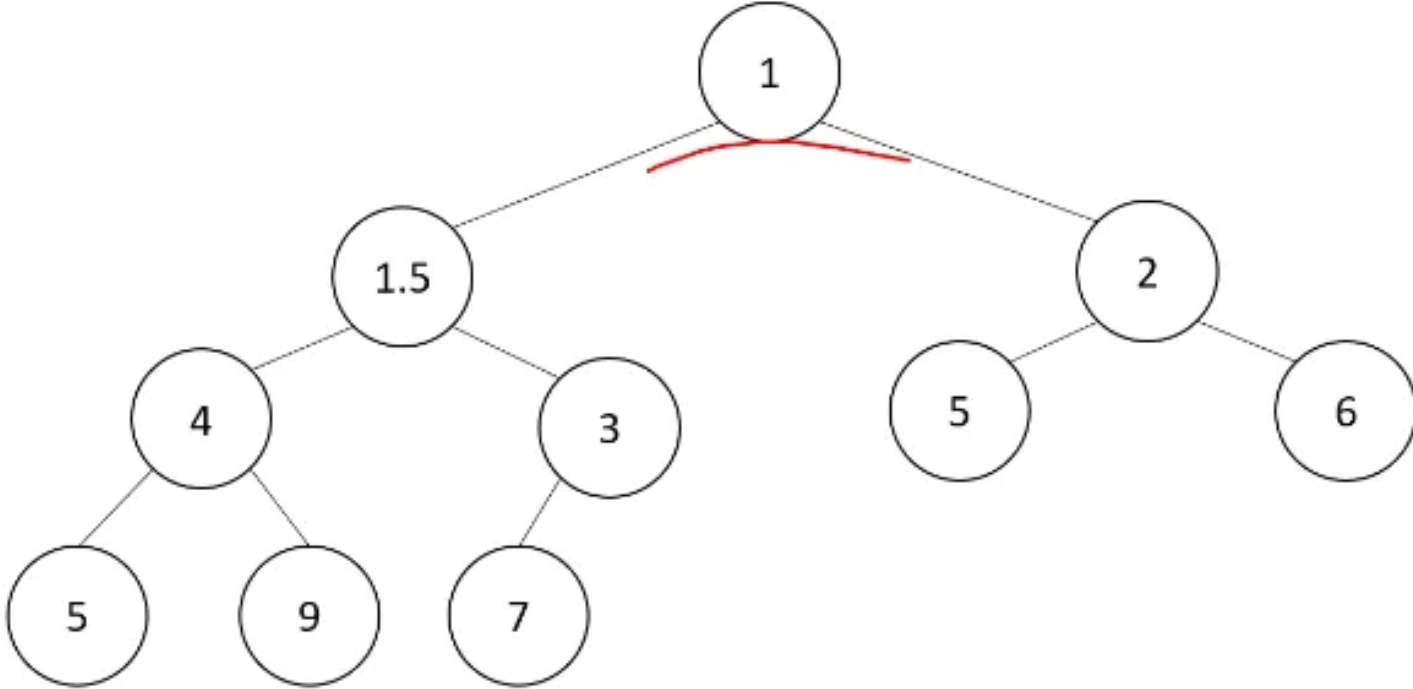
  • The value we want to delete is 1, but the node that needs to disappear is 7
  • We remove the last value, and replace 1 with that value
  • Then we just move it downwards by getting the minimum value of the children
    • u need the smaller one because otherwise heap property will be violated
  • We’re still doing 1 operation per level → log n

Java implementation