Binary tree

Definition

A binary tree is a type of tree where each node can have at most 2 child nodes.

• It is one of the most widely used tree structures and serves as the basis for many variations.

• A node does not have to have exactly two children — it can have 0, 1, or 2 children.
  • Thus, the maximum degree = 2.
• Even if two trees have the same root and the same child node, they are considered different trees if the child node is on the left in one and on the right in the other.

Tree 1:          Tree 2:

    A                A
   /                  \
  B                    B

• Even though both trees have the same nodes (A and B) and the same parent-child relationship (A → B), they are structurally different

Types

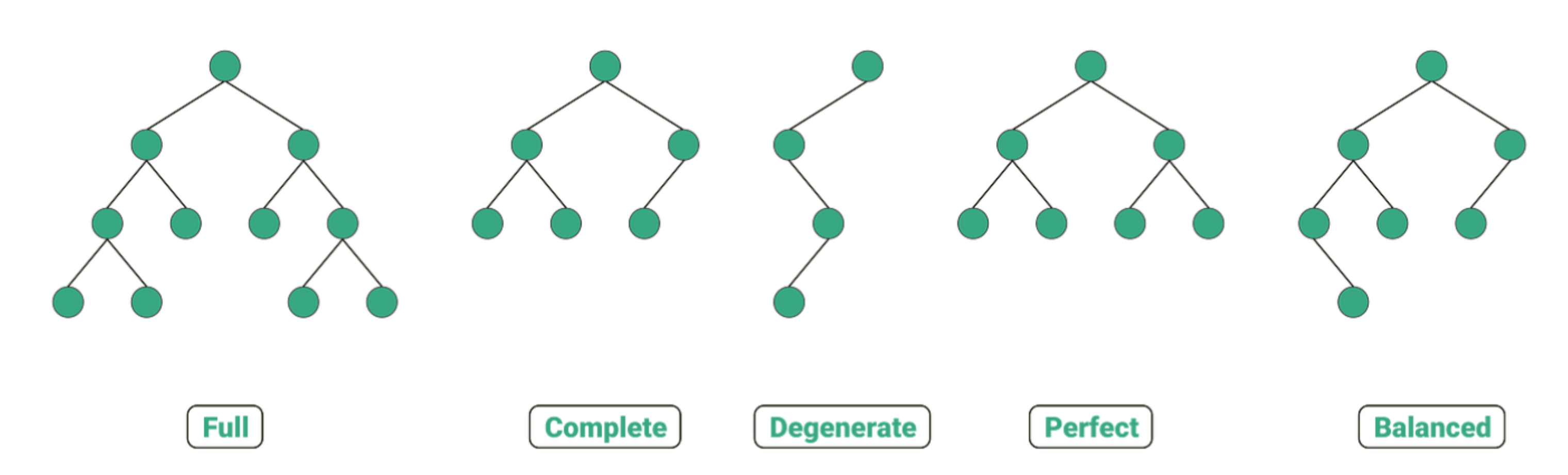
• Full binary tree (포화 이진 트리)
  • Every node has either 0 or 2 children.
  • All non-leaf nodes must have exactly two children.
• Complete Binary Tree (완전 이진 트리)
  • All levels are completely filled except possibly the last level
  • And the last level’s nodes are filled from left to right.
    • Well-suited for array-based representations (e.g., heaps)
• Degenerate / Skewed Binary tree (편향 이진 트리)
  • Each node has only one child, either left or right.
  • The structure becomes linear, leading to very poor search performance.
  • In the worst case, it performs like a linked list with time complexity O(n).
• Perfect binary tree (완전 포화 이진 트리)
  • All leaf nodes exist at the same depth.
  • All internal nodes have exactly two children.
  • The total number of nodes = $2^n-1$, where n is the height of the tree.
• Balanced binary tree (균형 이진 트리)
  • For every node, the height difference between the left and right subtrees is at most 1.
  • Ensures average-case search performance stays O(log n).
  • Common examples: AVL Tree, Red-Black Tree.